2030: 【一维数组】phi

给定一个正整数N，求所有不超过N且与N互质的数。互质的定义请参考后面的知识点提示。

一个正整数N(N≤100000)

每行一个与N互质的数，按从小到大的次序输出。

5

1
2
3
4

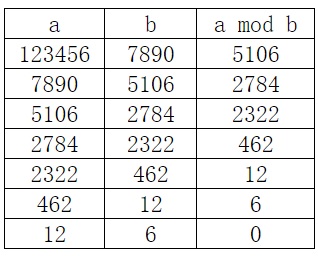
若A与B没有大于1的公因子，则称A与B互质。同样地本题也可使用数组记录要输出的数。求最大公约数可以用辗转相除法。辗转相除法又名欧几里德算法（Euclidean algorithm），乃是求两个正整数之最大公因子的算法。它是已知最古老的算法，其可追溯至3000年前。具体方法如下： 设两数为a、b(a＞b)，求a和b最大公约数(a,b)的步骤如下：用b除a，得a÷b=q……r1(0≤r1）。若r1=0，则(a,b)=b；若r1≠0，则再用r1除b，得b÷r1=q……r2 (0≤r2)。若r2=0，则(a，b)=r1，若r2≠0，则继续用r2除r1，……如此下去，直到能整除为止。其最后一个非零除数即为(a,b)。下面通过一个实例说明，其中“a mod b”是指取 a÷b 的余数。例如，123456 和 7890 的最大公因子是 6，这可由下列步骤看出：